NumPy Related

In NumPy, 1D array only have 1-d shape, and it can only be indexed by one index. For example,

a = np.array([1,2,3,4,5])
a.shape		# (5,1)
a[1]		# 2
a[0,1]		# IndexError: too many indices for array: array is 1-dimensional, but 2 were indexed

When we want to perform 1d array matrix multiplication, we can simply use @. For example,

a = np.array([1,2,3,4,5])
b = np.array([6,7,8,9,10])
# want a^T * b, no need to perform reshape
x = a @ b

When use @ for matrix and 1d array multiplication, the result is also a 1d array. For example,

A = np.ones((3,4))
b = np.ones(4)
c = A @ b		# returns a (3,) array
c = b @ A		# ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 3 is different from 4)

Therefore, if our objective is to get a scalar, it is ok to use 1d array in matrix multiplication.

Note that the order of @ can also affect the results. For example,

A = np.array([[1,2], [3,4]])
b = np.array([1,1])
c = b @ A 	# return [4,6], equivalent to b.T@A, treating b as a row vector.
c = A @ b 	# return [3,7], equivalent to A @ b, treating b as a column vector.

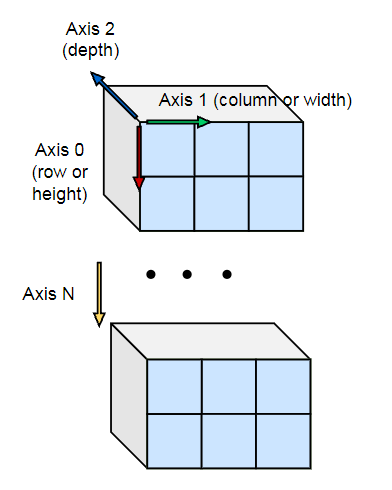
Array dimension

For N-dim array, we should be familiar with how the axis is defined. For example, if we have a 2d matrix, the row direction is axis=0 and the column direction is axis=1. We can also print the k-th axis data with

print(a[0,...,0,:,0...,0]) 	# fix other axis coordinate (for example 0) and only print k-th axis data. 	

Tensordot

For multi-dimensional array multiplication, we need tensordot, which in fact uses dot operation to generate new arrays. tensordot reduces the given axis dimensions based on a.shape x b.shape. For example, suppose we have two 3d array, we specify the axis to reduce

a = np.random.rand(2,3,4)
b = np.random.rand(4,2,3)
c = np.tensordot(a,b, axes=(2,0))

The original multiplication can generate 2x3x4 x 4x2x3 shape array, and we reduce the axis=2 in a and axis=0 in b, so that c has a shape 2x3 x 2x3. We can write c[i,j, m,n] = np.dot(a[i,j,:], b[:, m,n]), which is a scalar. The layout index is shown.

When there are multiple axis, for example,

d = np.tensordot(a,b, axes=((2,0), (0,1)))

d has a shape 3x3. We have d[i,j] = np.sum(a[:,i,:] * b[:,:,j]), which is the sum of elementwise multiplication. Here a[:,i,:] and b[:,:,j] are matrices with shape 2x4 and 4x2. This shape follows the natural order of the original array. However, we cannot use this shape to do elementwise multiplication and then sum. So we should specify the axes order. We should use axis=2 of a to multiply axis=0 of b. Therefore, we actually perform 4x2 and 4x2 elementwise multiplication and them sum them up. The code will report error if we use

d = np.tensordot(a,b, axes=((2,0), (1,0)))
# ValueError: shape-mismatch for sum

Although we eventually sum the elementwise multiplication, we should ensure every corresponding axis has the same dimension.

• Understanding tensordot

• Matrix multiplication on 4D numpy arrays

• Tensordot — Multidimensional Dot Product — Explained

Matrix multiplication with tensordot

A 2d matrix multiplication can better explain tensordot works. Suppose we have

A = np.random.rand(3,4)
B = np.random.rand(4,3)
C = A @ B
D = np.tensordot(A,B, axes=(1,0))	# C is equivalent to D

When we compute C[i,j], we need to perform dot product of A[i,:] and B[:,j]. Therefore, we in fact sum over axis=1 of A and axis=0 of B in matrix multiplication. Both A[i,:] and B[:,j] are 1d vectors, so the dot product is easy to understand. We multiply and sum them to obtain a single value as C[i,j].

The same applies to multiple axes in the previous example. We can think a[:,i,:] and b[:,:,j] as elongated vectors. We multiply and sum them to obtain a single element d[i,j] in the new matrix.

Tensordot with custom multiplication

Suppose we have a 4D matrix times 2D matrix:

A = np.random.rand(m,n, p,q)
B = np.random.rand(m,n)

Then A is a 4D matrix with A[m,n] as new pxq matrix. We want the first two dimensions of A to follow the arithmetic rule of matrix multiplication. In other words, we want C = A*B such that C still have mxn x pxq and C[m,n] is pxq matrix, but C[i,j] is obtained by $\sum_{k=1}^n A[i,k,:,:] \times B[k,j]$. We simply treat each (m,n) blocks of A as a number and perform matrix multiplication. We can write

C = np.tensordot(A, B, axes=(1,0)).transpose((0,3,1,2))

to obtain the result. Note that we need to rearrange the axis because tensordot by default gives mxpxqxn array. Similarly, if we have

D = np.random.rand(n,m)

and perform E = D*A with $E[i,j] = \sum_{k=1}^m D[i,k] \times B[k,j,:,:]$, we can write

E = np.tensordot(B, A, axes=(1,0))

without doing transpose because the dimension is correct.

However, if we have

G = np.random.rand(q,r)

and we want to obtain F: mxn x pxr, where F[m,n] is obtained by multiplying A[m,n, :,:] G. The latter is a standard matrix multiplication. We can write

F = np.tensordot(A, G, axes=(3,0))

without doing transpose.

Note: the key to use tensordot is to figure out which axes of A and B are going to be added and eliminated. Then we rearrange the axis of the result if necessary.

SciPy Related

SciPy optimization

In SciPy optimization, we can use minimize function to optimize multivariable problem. SciPy minimize provides many algorithms to perform optimization, such as 'BFGS' and 'SLSQP'. We can specify which algorithm to use in the attribute method. Note three things:

• Every method can have its own option settings, for example, maximum iteration and tolerance. We refer to SciPy Optimize API reference for more details.
• Not every method can solve the same problem. For example, BFGS can only solve unconstrained optimization. For constrained optimization, SciPy provides three methods: 'trust-constr' , 'SLSQP' and 'COBYLA'. The default method for constrained optimization is 'SLSQP'. For more details about unconstrained and constrained optimization, we refer to Optimization User Guide.
• The constraints in SciPy can be formulated as LinearConstraint and NonlinearConstraint.

The objective should be a scalar. The decision variable is a 1d array. So the Jacobian is also a 1d array.

The constraints’ Jacobian should be a $(m\times n)$ sparse matrix. We can from scipy.sparse import csr_matrix.

Note that SciPy optimization also provides other useful tools such as global optimization, root finding, least square fitting, linear programming, assignment problem. We can simply use existing APIs. There is no need to reformulate these problems to optimization problems and use minimize.